This puzzle can arguably be thought of as a mix of a crossword (without clues) and futoshiki (but with letters). It is presented as a grid with inequalities between cells and a few given letters. This implies we need to figure out how to fill the rest of the grid by inferring the constraints.

The key realization is that the grid must be filled with symbols for elements on the periodic table, as clued by the title. We may also notice that all the unchecked squares given in the “crossword” are single letter element symbols to help with this realization. While filling the grid, we may further infer that the outside red numbers are skyscraper constraints on the atomic numbers of the elements and the black inequalities are simply on the letters themselves. This is supported by the rules which show that black constraints are always single letters and red constraints may be single or double letters.

The full constraints are:

1. Black inequalities compare adjacent letter weights by A1Z26.
2. Red inequalities compare atomic numbers of adjacent elements read both across and down as in a crossword.
3. No element symbol appears twice. (All red boxes are unique.)
4. Red numbers are skyscraper values on how many elements are “visible” in that row or column.

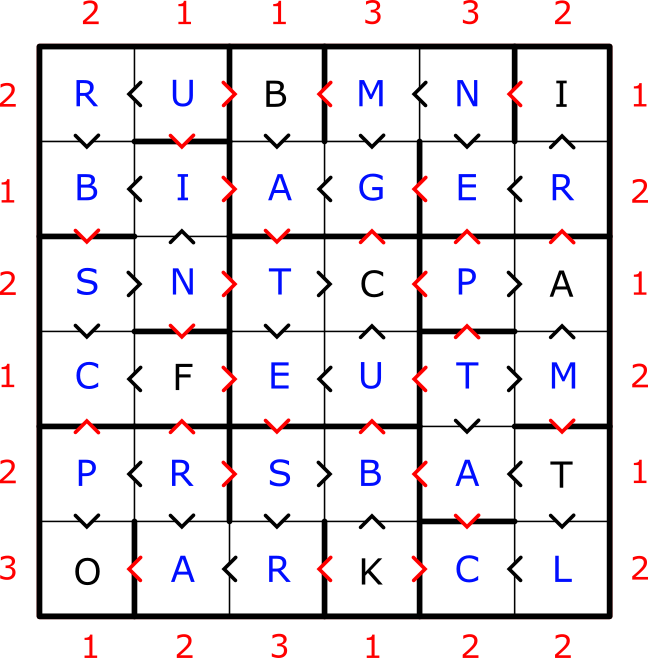
After solving the grid, we can read the diagonal on the final grid to get RITUAL, which is the final answer.

Example solve path

A walkthrough of one possible solution path is written out, though other deductions can be made. Cells are referred to by their row and column numbers.

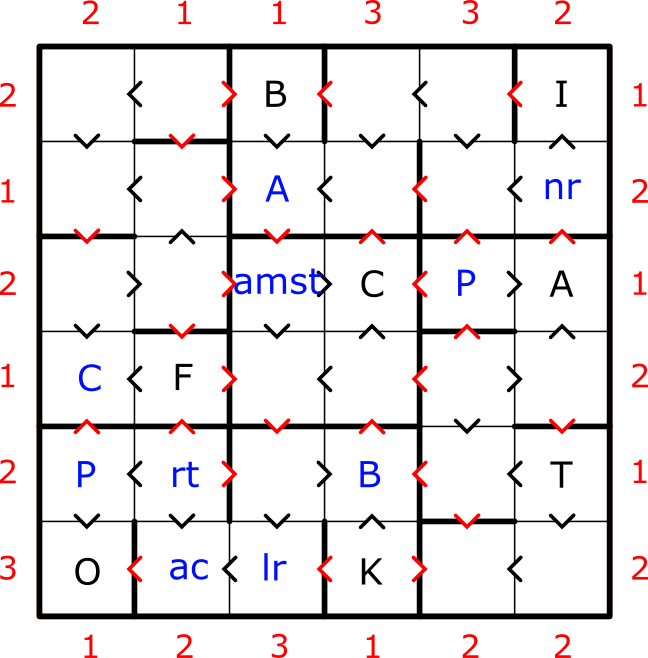
1) A few letters may be filled in quickly as there exist no other element symbols that can fill the location. Ba must be in R1C3 down by letter inequality of R1C3 (B) > R2C3 (A). Only element Bk has k as the second letter in R5C4 (B) and R6C4 (K). Only C in R4C1 satisfies the letter inequality with R4C2 and is still a valid element. There are five elements with O as the second letter for the down element in R5C1 and R6C1. However only one of them has a first letter greater than O so by letter inequality only Po may start in R5C1 (P) down. By cross-referencing elements beginning with P in R5C2 with elements that have an atomic number between that of O (R6C2) and K (R6C3) we get several possibilities for R5C2, R6C2, and R6C3. Noting that only single letter elements can go in unchecked boxes, only P in R3C5 does not conflict with (_C) in R3C3 and R3C4 by element inequality constraint.

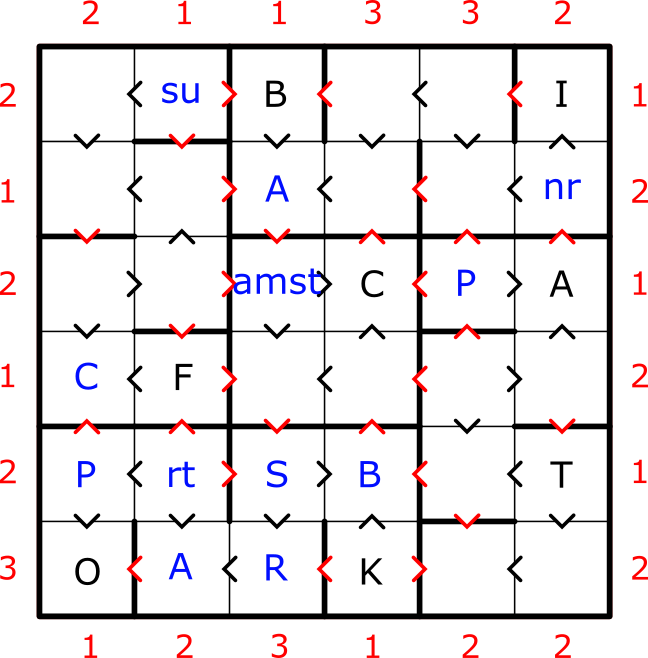
2) Only S or U from the set of possible single letter elements may go in R1C2 to satisfy the skyscraper inequality with R1C6 and still provide valid elements. By cross-referencing element symbols using R6C3 and R5C4 we deduce that R5C3 may only be S or T. However if Tl were in R[5-6]C3 it would break C3 element inequality with Ba therefore forcing most of the bottom left.

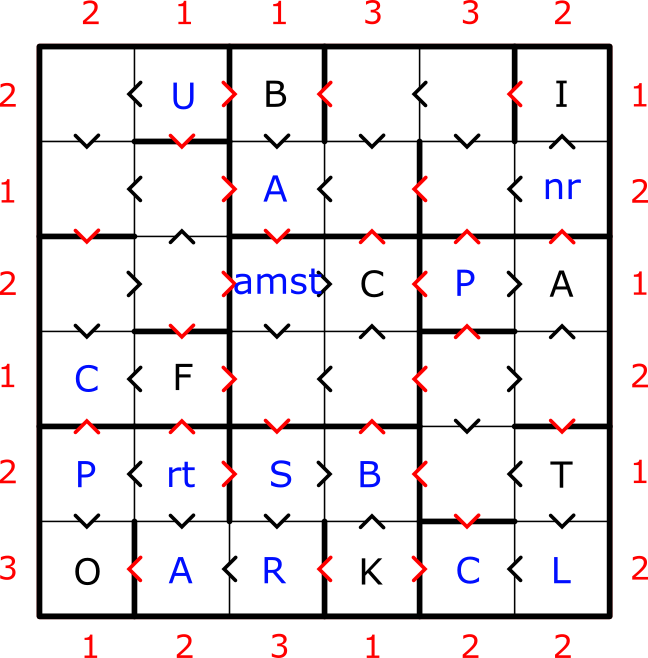
3) R1C2 must be U to satisfy the skyscraper inequality in C2, given the atomic numbers of R[5-6]C2. There are only a few elements in R6 that have atomic numbers smaller than K (Cl, Si, Ne, Na) however only Cl satisfies the letter inequality.

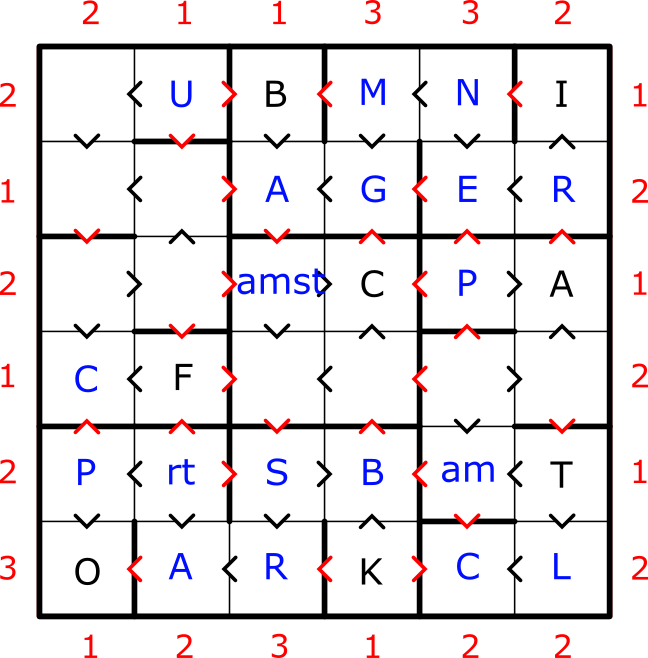
4) There are few double letter elements with a lower atomic number than P in R[1-2]C5 (He, Li, Be, Ne, Na, Mg, Al, Si). However most of the options break the needed letter inequality (Be), cause a repeat of an element with R[1-2]C1 (Li, Si), not yield a valid element in R[1-2]C1 (Na, Mg), or satisfy R2 skyscraper constraint (Al). So by process of elimination we can deduce that R[1-2]C5 should be either Ne or He which forces E in R2C5. However having H in R1C5 would not satisfy R1 letter inequalities so R1C5 must be N. Finally for the top right portion, only M in R1C4 works because it satisfies inequalities while not requiring using any element symbol twice. This forces the rest of the top right portion. We can also note some options in R5C5 based on R5 skyscraper constraints for elements ending in (_T).

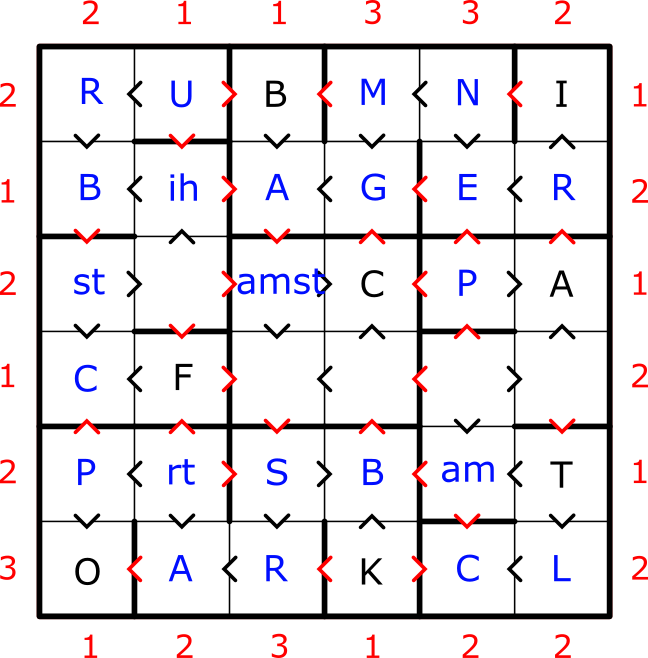
5) The first element in R1 must have a smaller atomic number than I, leaving only Cu and Ru possible for those cells. However Cu would force the first element in C1 to be Ca which would conflict with resolving the C1 skyscraper constraint with Po in the bottom left and element inequality with (_C) in R[3-4]C1. Therefore R1C1 is R and the top left element is Ru. R2C1 may be one of b, h, or e to create an element beginning with R in upper C1 that also has a smaller atomic number than Po in lower C1. However only Rb in R[1-2]C1 would not conflict with skyscraper inequalities in R2 and later in C2 along with letter inequalities.

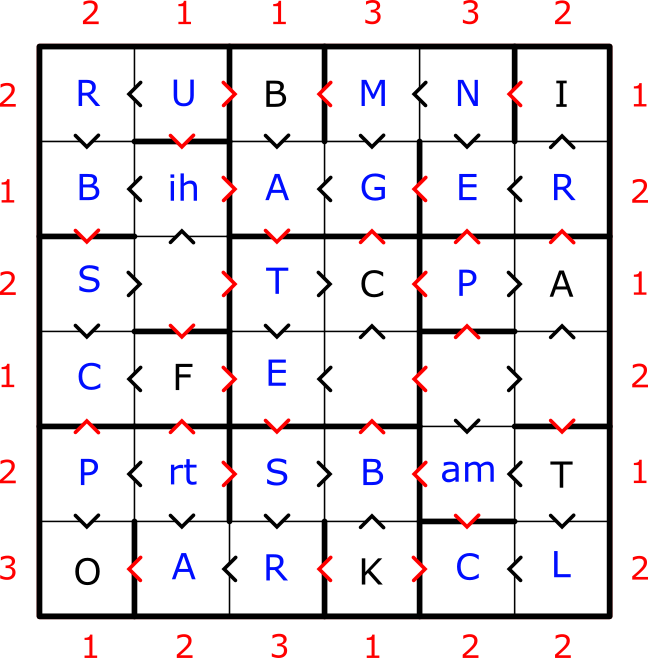
6) By C1 element inequalities, R[3-4]C1 is Sc as it must be between Rb and Po. Revisiting R3C3 in the center section, we deduce T in R3C3 by process of elimination since there are only 4 elements with letters (_C). Sc is used in R[3-4]C1, Ac breaks letter inequality, Mc breaks R3 skyscraper constraint. R4C3 is then E to satisfy the C3 element inequality between Ba and Sr.

7) There are only a few gaps remaining in the grid from this point. Multiple combinations of constraints can be used; only one solution satisfies all the rules.

Author's Notes

An early draft of this puzzle was written for our internal potluck. The puzzle went through a few versions though the main idea of using elements in a crossword-like fashion remained the same.

It was tricky tuning the uniqueness of the fill using all 118 possible elements. I considered making the grid larger to fit in a different extraction or entangling with another puzzle idea I had floating around. However the entanglement for the latter felt a bit arbitrary and for the former I was limited by the awful brute force script I wrote to check uniqueness. The ideas I had broke in a 6x6 grid. The current grid is actually unique without the given B and I in the first row, but it felt more grindy and additional single letter elements helped break-in. The skyscraper clues were left partly redundant to confirm elements as well, though some are needed for full uniqueness. Considering my original notes for this puzzle included “I am not sure this is constructable to be unique,” I am pretty happy with the final version.

There was a huge gap in testsolve times based on how much the title clued elements so we had to find something appropriate and within title constraints for Mystical Plaza. This meant that this was one of the puzzles that forced title constraints on much of the other puzzles in this round (apologies to the authors of Hexes and Spells).